softmax分类器是神经网络中最常用的分类器。它是如此简单有效,所以十分流行(这篇文章面向初学者,高手勿喷)
什么是softmax
对于一个输入x, 我们想知道它是N个类别中的哪一类
假设我们有一个模型,能对输入x输出N个类别的评分,评分越高说明x是这个类别的可能性越大,评分最高的被认为是x正确的类别。
然而,这样的评分范围很广,我们希望把它变成一个概率,而softmax就是一个能将\((-\infty,+\infty)\)的一组评分转化为一组概率,并让它们的和为1的归一化的函数(squashing function),而且这个函数是保序的,原来大的评分转换后的概率大,而小的评分对应的概率小。
为了达到这个squashing的目的,softmax 被定义为: \[
softmax(s_i) = \frac{e^{s_i} }{\sum_{j=1}^{N}e^{s_j} } \qquad (i=1,\cdots,N)
\]
其中\(s_i\)表示模型对输入x在第i个类别上的评分值,\(e\)指数的作用是将\((-\infty,+\infty)\)的评分变为\((0,+\infty)\),而不影响相对大小关系,而分母的求和是用来归一化的,使得它们加起来等于1
这样就可以将一组评分转化为一组概率,总概率和为1,而且保持相对大小关系。
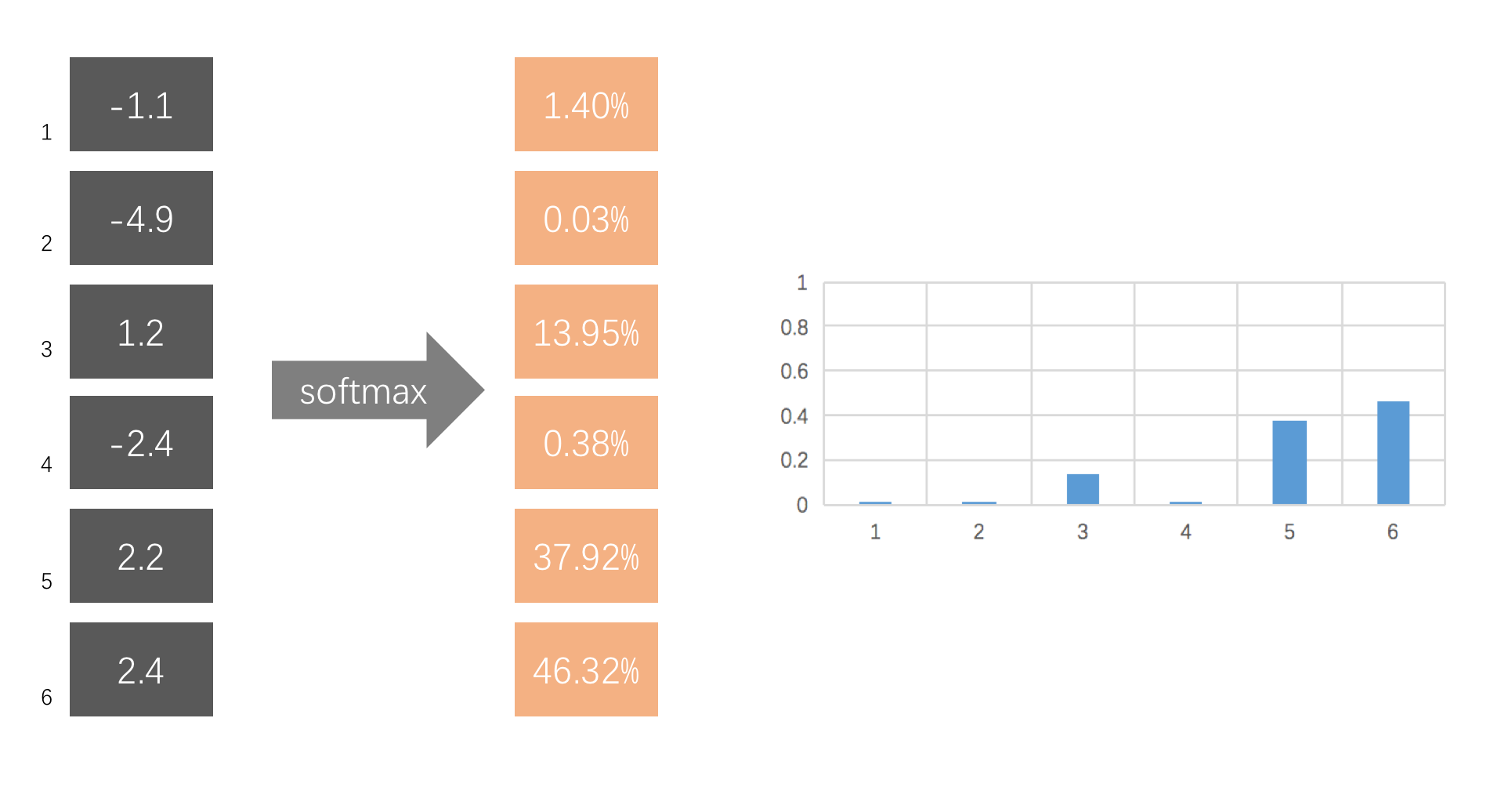
举个例子,下图的softmax将6个评分转化为一组概率
线性模型
如果单讲softmax这里已经结束了,它不过是一个squashing function
但这对一个分类器是不完整的,我们想知道前面这个评分模型怎么做,如果前面的模型不合理,加上softmax也没有任何意义,因此前面这个评分模型才是整个softmax分类器的关键。本节带大家认识线性模型
线性模型想法很简单,对于一个有n个属性的输入\(x\),它是i类别的评分被认为可以被\(x\)属性值的线性组合(加权和)确定,线性组合的组合系数(向量)记为\(\theta_i\)。
\[
x=\left( \begin{align}
& {x_1} \\
& {\vdots} \\
& {x_n} \\
\end{align} \right)
\] \[
\theta_i = (\theta_{i1},\cdots,\theta_{in})
\] \[
score_i= \theta_ix=\theta_{i1}x_1 +\cdots+\theta_{in}x_n
\] \[
i=1...N(假设有N类)
\]
带核函数的模型
线性模型简单,但是适用性有限,很多时候直接对属性进行线性评分是不合理的。可能不同属性之间有非线性的关联,单个属性值与评分之间也不一定是单调的线性关系,比如可能是中间大,两边小。因此我们需要考虑更复杂的模型,这里介绍一种基于已有数据的评分模型:核模型
核模型没有直接去建模属性之间潜在的复杂关系,而是尝试用已知数据衡量新的输入。(和KNN有类似的思想)(顺便提一下,支持向量机中的核技巧也是类似的思想,SVM提到的各种空间映射,各种对偶的推导,都是其花哨的外表,而不是其基于数据的本质)
核函数
进入正题前,先介绍一下核函数
核函数有很多种,这里介绍一种:高斯核,也叫RBF(径向基函数),被定义为:
\[
k(x,c) = e^{-\frac{ {\left\| x-c \right\|}^2}{2} }
\] 其中c是常量
下图是一个二维RBF函数示意图,最高点对应的是\(x=c\)时的取值 直观地看,x取值越接近c则核函数取值越大
根据RBF定义式,这个接近是用二范数,也就是欧氏距离度量的
核模型的评分
假设数据点越接近,则性质越相似(试问这种假设是否合理?)
然后,将评分定义为输入x到所有已知数据点接近程度(RBF值)的线性组合, 如果输入x和已知数据点是同一类别则组合系数大,而若是不同类别则组合系数小,那么当输入x接近同类数据点时评分就会高,而接近异类数据点时评分就会低(甚至为负)。
如此一来,就可以达到根据已知数据对输入的类别进行预测的目的(同类别评分高,而不同类别评分低)
考虑第i个类别的评分为\(score_i\),已知m个数据点,\({x}^{(1)},\cdots,{x}^{(m)}\)均为常量 \[ score_i={ {\theta }_{i} }\left( \begin{align} & k(x,{ {x}^{(1)} }) \\ & k(x,{ {x}^{(2)} }) \\ & \vdots \\ & k(x,{ {x}^{(m)} }) \\ \end{align} \right) \] \[ \theta_i = (\theta_{i1},\cdots,\theta_{im}) \] \[ i=1...N(假设有N类) \]
神经网络+softmax
基于RBF的核模型最大问题在上面越接近越相似的假设不一定成立
距离接近程度与评分不一定有简单线性关系,因为RBF考虑的是欧式距离,而数据可能是在复杂流形中分布的,例如一张对折的纸,上下挨着的两点欧式距离很近,但在纸张这个平面上的距离可能很远。
举个实际的例子,下面四副图片,第一幅是原图,右边三幅图片与第一幅图片的欧式距离相同(把图片像素看作向量分量计算距离),但他们的相似程度,或者评分应该相同吗?显然不是,第三幅图已经看不出是什么人了。 
由此我们看到了传统统计方法的瓶颈和理论缺陷,这种缺陷在高维数据上尤为明显(例如图片)。而后来的深度学习正是尝试突破这种瓶颈,尝试找到数据更本质规律的有益探索。
深度学习是基于在神经网络的,神经网络本质上就是对数据做非线性变换,使得变换后的数据可以经过线性模型正确分类,这是神经网络用于分类任务最基本的想法————变换数据,使其线性可分。
然而浅层神经网络并不成功,这种变换是难以学习的,让神经网络火起来的还是深度学习。至于深度学习是如何发现数据更本质的规律的,请期待后续文章。
训练方法
上面的内容讲到了各种模型,可是模型参数怎么确定呢, 下面讲三种方法
极大似然估计
上面讲过了,softmax输出的是一组概率,一个分布。 下面我们用极大似然估计的方法估计参数\(\theta\)(就是上文提到的\(\theta\))
假设当前输入为\({x_1,x_2,\cdots,x_m}\),\(y_i\)表示\(x_i\)的正确标签类别,似然函数可定义为: \[
L(\theta)=p(y_1 |\ x_1,\theta)\cdot p(y_2 |\ x_2,\theta)\cdots p(y_m |\ x_m,\theta)
\] 使得似然函数最大化: \[
\theta = argmax\ log(L(\theta))
\] 等价于: \[
\theta = argmin(-\sum_{i=1}^mlog(\ p(y_{i} |\ x_i,\theta)\ ))
\] 使得似然函数最大化的参数就是极大似然估计希望得到的参数,因此可以定义以下损失函数, 然后用梯度下降逼近最优解
\[
Loss = -\sum_{i=1}^mlog(\ p(y_{i} |\ x_i,\theta)\ )
\]
KL散度和交叉熵
对于一个输入\(x_i\),softmax输出的是一组概率\(q_i=[q_{i1},\cdots,q_{iN}]\),一个分布,这个分布和真实分布\(p_i\)(例如\(p_i=[0,0,0,1,0,0]\))存在差异。从信息熵的角度,我们可以直接用KL散度衡量两个分布的差异,然后最小化这个差异得到的参数\(\theta\)就是我们想要的结果。
因此可以定义损失函数: \[
Loss = \sum_{i=1}^N KL(p_i||q_i)
\] 根据KL散度的定义,可以展开为 \[
Loss = \sum_{i=1}^N H(p_i,q_i) - H(p_i)
\] \(p_i\)向量只有一个分量取值为1, 其它全为0, 因此 \(H(p_i)\equiv0\) 所以,可以仅用交叉熵\(H(p_i,q_i)\)表示损失函数 \[
Loss = \sum_{i=1}^N H(p_i,q_i)
\] \[
Loss = \sum_{i=1}^N p_{it}log(q_{it})
\] t表示\(p_i\)为1的那个分量
如果使用上一节定义的符号则可以改写为 \[
Loss = -\sum_{i=1}^mlog(\ p(y_{i} |\ x_i,\theta)\ )
\]
小结
从上面可以看出交叉熵,KL散度,极大似然估计这几种求解模型参数的方法,最终的结果都是等价的,由于交叉熵形式比较接近最终损失函数形式,人们默认交叉熵就是softmax分类器的损失函数。但是要注意,这三者的等价的关键在于标签只有一类是正确分类,这符合分类问题的定义。但如果你考虑的问题不是分类问题,或者标签是非平凡的(并不只有一类为1,其它全为0),再使用交叉熵就不合理了。
logistic 回归
logistic回归只是softmax应用在二分类问题上的特殊情况,其本质都是一样的,这里不再赘述。
支持原创,用我们自己的力量

